|
|
数字推理作为考生普遍难以拿分的考察部分,往往会被考生轻易的放弃掉,今年通过审核的考生达到105万,在如此激烈的竞争环境下,一分往往就能改变考生的命运,今天我们就告诉大家一个很好的复习方法,让您轻松拿分。 在日常的复习备考中,考生的主要任务不是看自己做了多少道题,而是熟悉各种题型,明晰解题思路,总结解题技巧,提高解题速度,提升应试能力。在此过程中,形成适合自己的便捷有效的解题技巧应该是重中之重。
(一)“三步走”法
总的来说,数字推理题的解题思路可以归纳为常用、好记、易学而又有效的 “三步走”:
第一步,在数列本身找规律
通过分析数列中所给数字的多少,根据数字大小变化的趋势,分析数列是不是常用的数列,如加法数列、减法数列、乘法数列、除法数列、分数数列、小数数列、等差数列、等比数列、平方数列、立方数列、开方数列、偶数数列、奇数数列、质数数列、合数数列、排序数列、摆动数列,或者是复合数列、混合数列、隔项数列、分组数列等稍微复杂的数列形式。为了解题方便,可以借助于题后答案所提供的信息,或是数列本身的变化趋势,初步确定是哪一种数列,然后调整思路进行解题。具体方法如下:
(1)先考察前面相邻的两三个数字之间的关系,在大脑中假设出一种符合这个数字关系的规律,如将相邻的两个数相加或相减,相乘或相除之后,并迅速将这种假设应用到下一个数字与前一个数字之间的关系上,如果得到验证,就说明假设的规律是正确的,由此可以直接推出答案;如果假设被否定,就马上改变思路,提出另一种数量规律的假设。另外,有时从后往前推,或者“中间开花”向两边推也是较为有效的。
(2)观察数列特点,如果数列所给数字比较多,数列比较长,超过5个或6个,就要考虑本数列是不是隔项数列、分组数列、多层级数列或常规数列的变式。如果奇数项和偶数项有规律地交替排列,则该数列是隔项数列;如果不具备这个规律,就可以在分析数列本身特点的基础上,三个数或四个数一组地分开,就能发现该数列是不是分组数列了。如果是,那么按照隔项数列或分组数列的各自规律来解答。
(3)如果不是隔项数列或分组数列,那么从数字的相邻关系入手,看数列中相邻数字在加减乘除后符合上述的哪种规律,然后寻求答案。
根据这种思路,一般的数字推理题都能够得到解答。如果有的试题用尽上述办法都没有找到解题的思路,而数列本身似乎杂乱无章,无规律可循,那么,就可以换用“第二步”。
第二步,求数列中相邻各数之间的差值
求数列中相邻各数之间的差值,采用层层剥茧的办法,逐级往下推,在逐级下推的差值中,一般情况下,经过几个层次的推导,都会找到数列内含的规律的,然后经过逐层回归,就可以很快求出空格所要的数字,使数列保持完整。根据笔者多年教学以及在各种培训班上授课的经验,一般的数字推理题,在第一步解决不了的话,在第二步运用层级推导的办法(实为多层级数列,属于复合数列中的一种)都可以解题。但是也有个别比较“刁钻”的试题,运用上述两种办法都解决不了的,就得用第三步了。
第三步,回到数列本身根据推算找规律
这次回到数列本身推导时,不能用惯常的思维和普通的数列知识了,而要换一种思路——看数列的后面项是不是它相邻的前几项的和(或差),或是前几项的和(或差)加上(减去)一个常数或一个简单的数列构成的。这样的数列常见于加减复合数列、加减乘除复合(摆动)数列,难度比较大,考生在复习备考时多做几道题、多总结,熟悉了其组合方式或内在的规律,此类数字推理题就不难解决。
需要说明的是:近年来数字推理题的变化趋势是越来越难,需综合利用两个或者两个以上的规律才能得到答案。因此,当遇到难题时,可以先跳过去做其他较容易的题目,等有时间时再返回来解答这些难题。这不但节省了时间,保证了简单题目的得分率,而且解简单试题时的某些思路、技巧、方法会对难题的解答有所帮助。有时一道题之所以解不出来,是因为我们的思路走进了“死胡同”,无法变换角度进行思考。此时,与其“卡”死在这里,不如抛开这道题先做别的题。做这些难题时,可以利用“试错法”。很多数字推理题不太可能一眼就看出规律、找到答案,而是要经过两三次的尝试,逐步排除错误的假设,最后找到正确的规律。
(二)“凑数字、找规律”法
一般而言,再难得数列运用上述方法都可以推导出结果的。但是近几年,不管是中央国家公务员的考试,还是地方性公务员的考试体(尤其是各省级的试题),出现了一些所谓的偏题、怪题,运用上述方法还不容易直接解题,甚至出现没法下手解题的情况,有的考生就采取了“放弃”,实不足取。这里再介绍一种非常有用的解题方法,可以说对所有的难题、偏题、怪题都有用,那就是“凑数字,找规律”。这里凑的数字的来源一是数列本身,即数列中的原数字(即通过数列中相邻的数字的计算,查找数列中各数之间隐含的计算法则,而这个计(运)算法则就是所要找的规律),二是数列中每一项的序数,即每一项在数列中的第1、2、3、4、5……项的项数(这是第一步走不通时,就想到将数列的每一项所在的顺序数与数列中的苏子对应起来进行计算,往往可以很顺当地找到规律的)。
1.利用数列中的原数“凑数字,找规律”
为了让考生掌握“凑数字、找规律”的这一方法,这里以2008年中央国家机关公务员录用考试《行政职业能力测试》中的5道数字推理题为例,作一讲解、演示:
〖例1〗157,65,27,11,5,( ) [2008年国考第41题]
A. 4 B.3 C.2 D.1
【解析】分析本题所给数列发现,这是一组呈现逐步递减趋势,而且递减的趋势越来越和缓的数列;更为要命的是这一组数字没有任何明显的规律,根本不是常规的平方、立方、减法等数列及其变式,一下子找不到思路,对此类试题,就可以考虑采用“凑数字,找规律”的思路求解。
根据上面总的提示及思路,要“凑”的数字首先在数列本身去找,要“找”的规律就是数字之间运算的法则。而要运算则最少必须有三个数字,那么可以尝试着对相邻的三个数字运用“凑”的方法进行计算。那就是说前三个数字157、65、27之间有什么样的关系呢?或者说65和27经过什么样的计算能得到157呢?(当然思考157和65之间经过什么样的运算能得到27、或157和27之间经过什么样的运算能得到65也可行,但是那样的话肯定要经过减法等运算,一是增加了解题的难度,二是容易出错,一般人运用加法、乘法计算时要比运用减法、除法快捷得多,而且不容易出错,那么在这里再给考生一句话,那就是在解数字推理,乃至于数学运算和资料分析题时必须把握一个原则:“能加就不减,能乘就不除”,即能用加法计算的尽量用加法计算,而不要用减法去运算;能用乘法的就尽量用乘法,而不用除法运算)如果能想到这一点的话,问题就变得简单多了,因为稍稍推算就可以发现它们之间有这样的运算65×2+27=157。那么再往后推一下,看第2、3、4个数字之间是不是也有这样的规律,演算一下发现第二组数字65、27和11之间也有同样的规律,即27×2+11=65。那么再用第三组数字验证一下是不是该数列都有这样的规律,如果第三组也有的话,那么这个运算法则就是本数列的规律了。经过推算发现第三组数字27、11和5也有同样的运算法则,即11×2+5=27,那么本数列的规律是:第一个数等于相邻的后一个数的2倍再加上第三个数。那么所求的未知数为11-5×2=1,选D。(这里以2008年国考的第41提为例向考生详细介绍了“凑数字、找规律”的基本思路和解题方法,讲述得比较详细甚至繁琐,下面各题主要是对这一方法的强化,就简化介绍思路了。)
〖例2〗[2008年国考第42题]
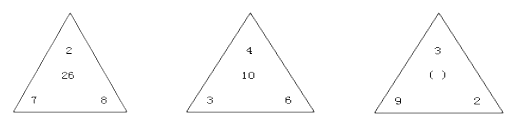
A. 12 B.14 C.16 D.20
【解析】尽管本题给的是三角形负载的四个数,小数字在周边,大数字在中间,也没有明显的规律,同样可以用“凑数字,找规律”的思路和方法求解。同上题,凑的数字同样首先在数列本身去找,要找的规律就是数字之间运算的法则。经过演算可以发现26=(7+8-2)×2,第二个三角形中也有同样的规律10=(3+6-4)×2,即本题数列的规律是:三角形内中间数字等于三角形底角两个数字之和减去顶角数字的差的2倍。按照相应的数字的位置和法则进行计算,可知所求未知数为(9+2-3)×2=16,选C。
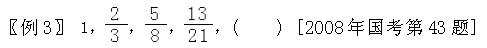
A. B. C. D.
【解析】尽管本题又换成了分数数列,数字间规律不明显,同样使用“凑数字,找规律”的思路和方法求解。对本题而言,凑数字时因为第一项是1,比较特殊,就从数字不大变化又比较明显的第二、三项开始查找、推算,凭对数字的敏感性可发现后一个分数的分子5正好是第一个分数的分子与分母2与3的和;那么就可以考虑到后一个分数的分母8是不是也可以从前一个分数的分子分母得到呢,经过凑数字可以发现8=2×3+2。那么往前延伸看前面的两个是之间是不是也有这样的规律呢,经过推算正好有此规律,那么再通过第三组即第3、4个分速进行验证,正好也有同样的规律:5+8=13,5+2×8=21。通过“凑数字”发现本题的规律是前一个数的分子分母之和为相邻分数的分子,前一个数的分子加上分母的2倍等于相邻数的分母,则所求未知数的分子为13+21=34,分母为13+21×2=55,即原数为34/55,选D。
〖例4〗67,54,46,35,29,( ) [2008年国考第44题]
A. 13 B.15 C.18 D.20
【解析】本题的思路同上,运用“凑数字,找规律”的方法可以发现本题的规律是相邻数的和是一个以11为首数的递减的连续自然数列的平方,则未知数为72-29=20,选D。
当然有的考生利用球相邻数之间的差值的方法去求解,求得相邻数之间的差值分别为13、8、11、6,就认为本数列的差值是一个隔项数列,即13、11是一列,8、6是一列,认为这是一个以2为公差的等差数列,那么下一个数就是9,还原上去可求得未知数为29-9=20,答案同样为D。在这里只能说明这是“歪打正着”属于碰巧。因为根据一般的思路,我们的猜想、推算是不是就是规律,一般来说必须经过三步:第一步猜想,第二步看下一个数列里面是不是也有同样的运算,第三步是验证,即看第三组数列中是不是也有同样的计算,有的话才能确认猜想的计算事故,说明要是只凭第一步和第二步就急急忙忙推算未知数,那是有特别大的危险性,出错率相当高,而且那往往是出题人设置的陷阱,对此考生一定要小心,且不可想当然解题。
〖例5〗14,20,54,76, ( ) [2008年国考第45题]
A. 104 B.116 C.126 D.144
【解析】本题比较难,规律更是不明显,但是结合答案所个数字分析数列可以发现本题数列递增比较快,但又不是特别快,就可以猜想其中隐含着平方或乘法的运算法则。由于乘法的运算不是很明显,也没有什么规律可寻,就先尝试平方的运算。突破口是20和54,因为要形成平方,这两个数一个少一个5,即52-5;另一个则多了个5,为72+5再往前往后延伸,发现前面是32+5的形式,后面是92-5,那么所求的数位112+5=126,选C。
2.利用数列中每一项所在的序数“凑数字,找规律”
有的数列看起来比较简单,实际上解起来很难,往往有无从下手之感,那么对企业可以用“从数字,找规律”的思路和方法去求解。对要“凑”的数字从数列本山找不到,或者利用原数列中的数字没法运算找不到规律时,就可以想到利用数列的每一项所在序数进行推导计算。对这类试题,如果把数列的每一项所在的序属与数列中的数字对应起来的话,本试题就变得相当简单。
〖例1〗0,6,24,60,( )
A.108 B.120 C.125 D.136
【解析】本数列看似简单,而且从数列中比较特殊的几个书,尤其是6、24、60可揣测知本数列中的四个数似乎与6或4有倍数关系,但是首项数为0,这种思路走不通(其实这是误导,或者说是出题人设置的陷进),说明此数列也不可能是等比数列。在没有直接的、有效的解题思路的前提下,就可考虑将数列中的各个数与其所对应的序列号1、2、3、4…联系起来尝试着推导,看能否找到某种规律或得到某些启示。把数列中的数与其对应的序列数1、2、3、4加起来(最好不要减,因为0-1=-1为负数,一般不好推导),得到1、8、27、64,其规律一下子就明朗了,即题干各数为自然数列1、2、3、4的立方依次减1、2、3、4所得,故最后一项为5的立方减5得120,答案为B。
〖例2〗-2,-8,0,64,( )
A.-64 B.128 C.156 D.250
【解析】本数列看似简单,但是解起来相当困难,似乎没法下手。因为从每一个数字前面的符号来看,是-、-、0、+,而不是-、+、-、+、……或+、-、+、-、……的形式,说明数列前面的符号不是(-1)n或(-1)n+1的形式;说明数列也不是立方数列(-2)3=-8的形式,因为下一步就没法往下推算了。可见这些思路都走不通。在实在找不到思路的情况下就应该想到换用“凑数字,找规律”的思路进行求解。通过上面的推算可知期望通过数列本身的数字凑出规律来是行不通的,那只好借助于数列的每一项所在的序数推导了。
将数列每一项的序数1、2、3、4与数列中的数字联系起来,结合上面的判断可知,数字前面的负号和正号相连出现,并且以第3项的0为拐点由负号转为正号,说明正负号是数字前面的系数运算(相减)的结果,而且有一个数即减数保持不变,而被减数是逐步递增的,到第3项为0,说明被减数和减数正好相等,其结果就为0,这里已经有一个虚数3了,那么第3项的系数就是3-3=0了,0乘以任何数的结果都为0,与数列中的数正好对应上。
第3项之前的各数为负,第3项为0,第4项为正数,说明减数3是一个常量,而被减数是由小到大递增的,而第1、2项的叙述正好为1、2,那么可以推知每一项的系数分别为1-3=-2,2-3=-1,3-3=0,4-3=1,即本数列的系数是(n-3)的形式(其中n为自然数),那么要求的第五项的序数则为5-3=2。
另外,根据数列中的数字2、8、64说明本数列是一个次方数列,而系数已经推知了,那么该次方数列的原数就可以用数列中的数除以系数计算得知了,那么第1项为(-2)÷(-2)=1,第2项为(-8)÷(-1)=8,第4项为64÷1=64,根据第1、2、4项分别为1、8、64可知这是一个以1为首位的连续自然数的3次方的数列,即n3的形式,那么第3项就是33=27,第5项则为53=125,乘以系数2即为250,选D。
本题将系数与次方数列整合在一起,那么整个数列就是(n-3)n3的形式
[ 本帖最后由 蘋^氺^缃漨 于 2008-10-31 14:49 编辑 ] |
|